Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history · 165 k Answer Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams Find the range of 6k 1k 314 Find the rangeFind the range of function f defined by Solution to Example 4 The domain of this function is the set of all real numbers The range is the set of values that f(x) takes as x varies If x is a real number, x 2 is either positive or zero Hence we can write the following x 2 ≥ 0 Subtract 2 to both sides to obtain x 2 2 ≥ 2 The last
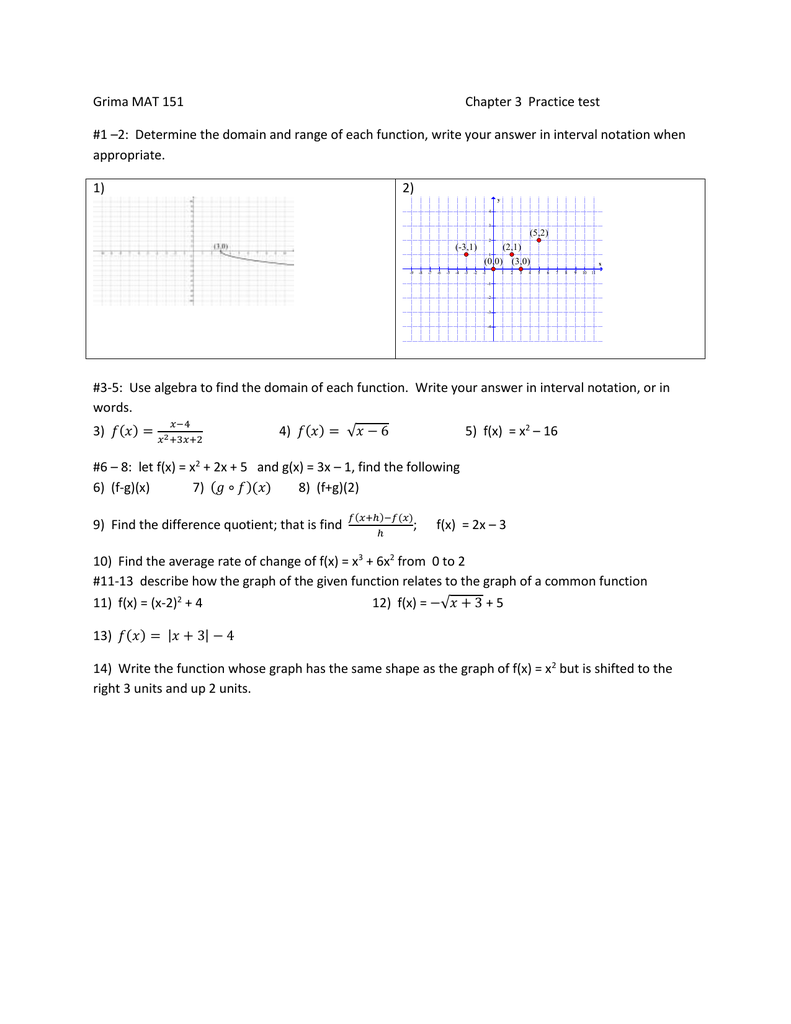
Mat 151 Chapter 3 Mini Practice Test
F(x)=x/1+x^2 find domain and range
F(x)=x/1+x^2 find domain and range- · Find the domain and range of f(x)=x3/2x1 doubts101 doubts101 Mathematics Middle School answered Find the domain and range of f(x)=x3/2x1 please show steps 1 See answer doubts101 is waiting · Best Answer f(x) = 1 / √(9 x^2) Since the denominator can't = 0 , x cannot be 3 or 3 And since we can't take the square root of a negative number, any x values < 3 or > 3 make the square root nonreal
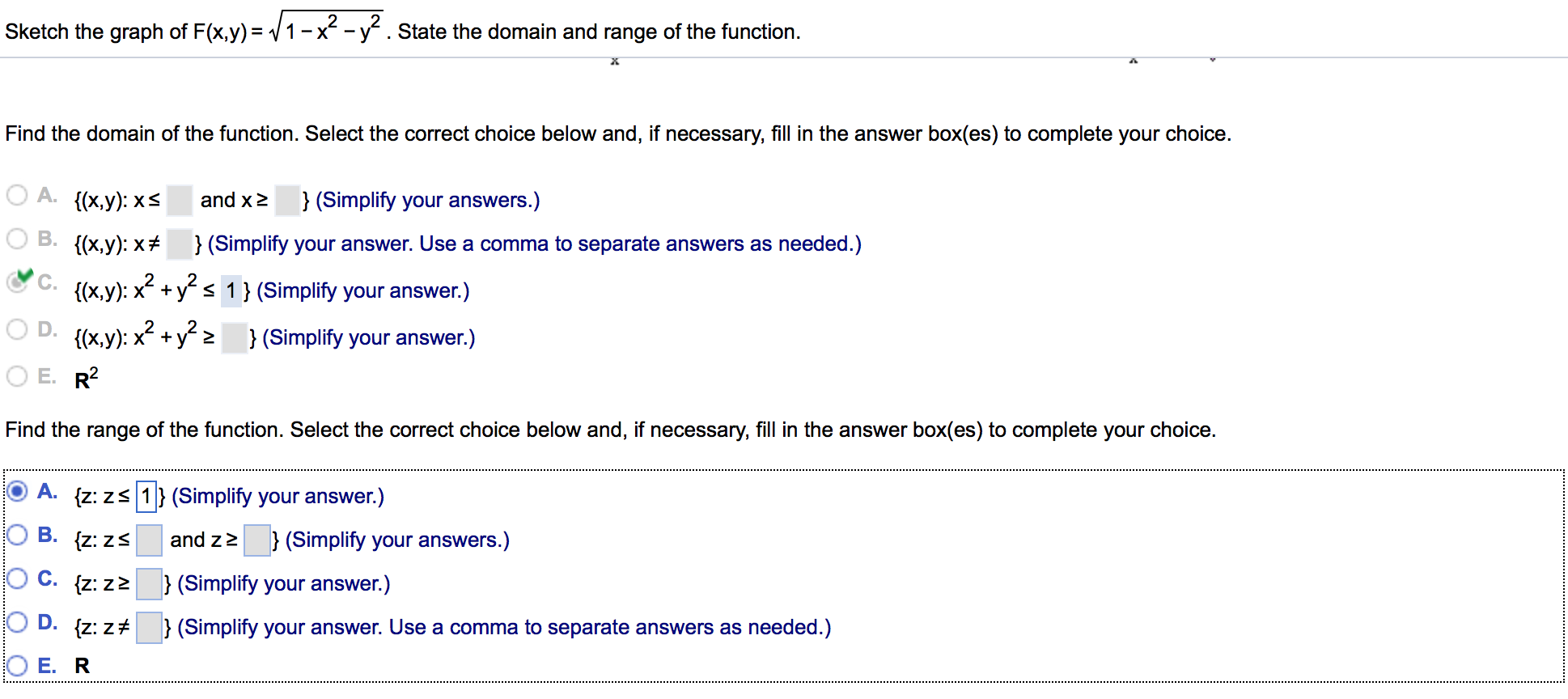



Solved Sketch The Graph Of F X Y Squareroot 1 X 2 Chegg Com
/11/13 · find the inverse of f(x)=(1/2x2)sq Determine whether it is function and state its domain and range asked Nov 23, 13 in ALGEBRA 2 by payton Apprentice domainofafunction · Rule The domain of a function on a graph is the set of all possible values of x on the xaxis For domain, we have to find where the x value starts and where the x value ends ie, the part of xaxis where f(x) is definedLet D be the domain of the real valued function f defined by f ( x ) = 2 5 − x
· Find the domain and range of the real function f(x) = x/1x^2 ━━━━━━━━━━━━━━━━━━━━━━━━━ ️Given real function is f(x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R ️Let f(x) = y ️y = x/1x^2 ️⇒ x = y(1 x^2) ️⇒ yx^2 – x y = 0 ️This is quadratic equation with real roots ️(1)^2 – 4(y)(y) ≥ 0Algebra Find the Domain and Range F (x)=1/ (x^2) F (x) = 1 x2 F ( x) = 1 x 2 Set the denominator in 1 x2 1 x 2 equal to 0 0 to find where the expression is undefined x2 = 0 x 2 = 0 Solve for x x Tap for more steps Take the square root of both sides of the equation to eliminate the exponent on the left side x = ± √ 0 x = ± 0This is a revised answer!
Find the domain and range of the function $$f(x) = \sqrt{x^2 25} $$ and $$ f(x) = \sqrt{25 x^2}$$ · Find the range of f (x) = 1x2 To find The range of the expression ? · To find the domain and range of function Explanation So, the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f (x) = 1/√x−5 Now for real value of




Find The Domain And Range Of The Inverse Of The Given Chegg Com




Domain Of Function F X X 1 5 X Donimain
Determine the equation of the vertical asymptote for the graph of this function, and state the domain and range of this functionf(x) = ln(x 2) 4 asked Sep 15, 19 in Mathematics by Megatron algebraandtrigonometryThe domain−4,4 Range f (x) is maximum at x = 0,f (x) = 4 And f (x) is minimum at x= 4,f (x)= 0 Range 0,4 Hence, this is the answerThe range of x 2 x 1 x 2 − x 1 is If f ( x ) = 1 − x 2 , then what is the largest number in the range of the function f ?




Answered Mac 114 1 Use The Vertex And Y Bartleby




F X 2x 1 Find Domain And Range Brainly In
F(x) = x 2 The function f(x) = x 2 has a domain of all real numbers ( x can be anything) and a range that is greater than or equal to zero Two ways in which the domain and range of a function can be written are interval notation and set notationLet y = f(x) be a function Range is all real values of y for the given domain (real values of x) Let us look at some practice questions to understand how to find domain and range of a function Practice Questions Question 1 Find the domain of 1 / (1 − 2sinx) Solution 1 − 2sin x = 0 2sin x = 1 sin x = 1/2 sin x = sin π/6 · Find the domain and range of the following functions f(x) = 1 x 2 Solution For any values values of x, the function will give defined values It will never become undefined So, domain is all real values that is R The range of x 2 lies between 0 to ∞ But we need find the range of 1 x 2 0 ≤ x 2 ≤ ∞ Multiplying




Ex Find The Inverse Of A Square Root Function With Domain And Range Youtube




Hence The Range Is Illustration 1 10 Find The Domain And Range Of F X Vx2 3x 2 Sol For Domain X2 3x 2 Or X 1 X 2
Find the domain and range of f(x)=x1/x^24 1 Log in Join now 1 Log in Join now Ask your question anggandako123leche anggandako123leche 1410 Math Senior High School Find the domain and range of f(x)=x1/x^24 1 See answer · All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that Range f (x) is 0 or negative numbers, Hence, Range = (−∞, 0 Ex 23, 2 Find the domain and range of the following real function (ii) f (x) = √ ( (9 −x^2)) It is given that the function is a real functionThe range is also determined by the function and the domain Consider these graphs, and think about what values of y are possible, and what values (if any) are not In each case, the functions are realvalued—that is, x and f(x) can only be real numbers Quadratic function, f(x) = x2 – 2x – 3



Graphing The Basic Functions




Find The Domain And Range Of The Function Defined By F X 1 9 X Please Help Me Brainly In
F (X) = 1 – 3X 2) Find the vertex, axis of symmetry, domain and range of the graph of f (X) = · quency table which shows the distribution of data with respect to all types of books Round your answers to the nearest whole percent Graph the circle First plot the center and then plot a point on the circle x2y2−4x−6y4=0 Find the circle about itWhat is the domain and range of the real function f(x)=1/(1x^2)?




Functions Composite Ppt Download




Find The Domain And Range Of The Function F X X 1 X 2 Brainly In
X, y ∈ R Let y = f (x) Then y = 1 1 − x 2 means that because the denominator cannot be 0 So the domain of f is To find the range, get x in terms of y So clearly, Then because it is a squMath Precalculus Precalculus questions and answers ) Find the average rate of change of f (X); · Hello sir, Please explain this sum, Find the domain of the functions i) f(x) = 1/√(x^2 5x 6) ii) f(x) = x^22x1/x^28x12 4x1 then x = mod(2xx)=4 where represent greatest integer function find domain of √x^25x6 Find range




Find The Domain Of A Function Defined By An Equation College Algebra




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube
The same applies to the vertical extent of the graph, so the domain and range include all real numbers Figure 18 For the reciprocal function f ( x) = 1 x , f ( x) = 1 x , we cannot divide by 0, so we must exclude 0 from the domain Further, 1 divided by any value can never be 0, so the range also will not include 0When the given function is of the form f(x) = 2x 5 of f(x) = x 2 – 2, the domain will be "the set of all real numbers When the given function is of the form f(x) = 1/(x – 1), the domain will be the set of all real numbers except 1 In some cases, the interval be specified along with the function such as f(x) = 3x 4, 2 < x < 12 HereAnswer by lwsshak3 () ( Show Source ) You can put this solution on YOUR website!
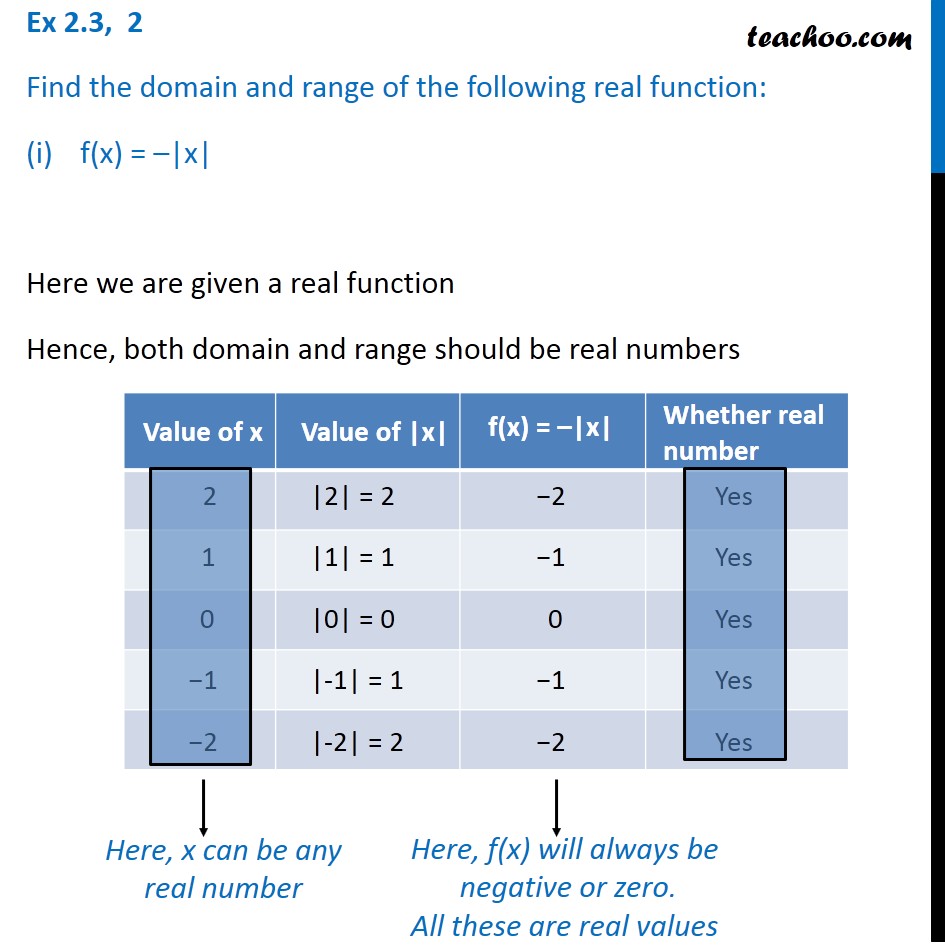



Ex 2 3 2 Find Domain And Range I F X X Chapter 2




Calculus Practicals Maxima And Minima Derivative
Find the domain and range of the following function f(x) = (x2)(5x) Maharashtra State Board HSC Science (Electronics) 11th Textbook Solutions Concept Notes & Videos 325 Syllabus Advertisement Remove all ads Find the domain and range of the following function f(x) = (x2)(5x) Mathematics and Statistics Advertisement Remove allAnswer to Find the domain and range of the function f(x, y) = V 16 x2 y2 Domain •{(x, y) x2 y2 < 16 • {(x, y) x2Find Domain and Range of real functions (1) `f(x)=(x2)/(3x)` (2)`f(x)=1/sqrt(x5)` (3) `f(x)=x/(1x^2)`




The One To One Function Is Defined Below F X Chegg Com




Find Domain And Range Of F X X 1 X 2
Answer f (x) = −∣x∣ We know, ∣x∣ = x,x≥ 0 ∣x∣ = −x,x < 0 Since, f (x) is defined for x ∈ R, the domain of f is R It can be observed that the range of f (x) =−∣x∣ is all real numbers except positive real numbers Therefore, the range of f is (−∞,0 Answer verified by Toppr Upvote (0)Domain\y=\frac {x^2x1} {x} domain\f (x)=x^3 domain\f (x)=\ln (x5) domain\f (x)=\frac {1} {x^2} domain\y=\frac {x} {x^26x8} domain\f (x)=\sqrt {x3} domain\f (x)=\cos (2x5) domain\f (x)=\sin (3x) functiondomaincalculatorSech(x) = 2 / (e x e x) (∞ , 0) U (0 , ∞) More Find domain and range of functions , Find the range of functions , find the domain of a function and mathematics tutorials and problems , Step by Step Calculator to Find Domain of a Function




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




Mat 151 Chapter 3 Mini Practice Test
The range is defined as the set of all valid y values or The range is the set of values that correspond with the domain If we the first find the domain of the function ie the set of values where function is defined Then y approaches to 1 · Misc 5 Find the domain and the range of the real function f defined by f (x) = x – 1 Here we are given a real function Hence, both domain and range should be real numbers Here, x can be any real number Here, f (x) will always be positive or zero Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note · Find the domain and the range of the function $\log_{\csc x1}(2\sin x\sin x^2)$,where $$ denotes the greatest integer function 0 what is the domain of $\frac{1}{\sqrt{xx}}$ where x denotes the greatest integer function and find the range




Find The Domain And Range Of F X 1 Sqrt X 2




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2
· Best answer We have 2x x2 = (x2 2x 1) 1 = 1 (x 1)2 Thus, ∞ < 1 (x 1)2 ≤ 1 ⇒ cot1( ∞) < cot1(1 (x 1)2) ≤ cot1(1) ⇒ 0 < cot1(1 (x 1)2) ≤ π/4 Hence, the range of the function = (0, π/4} Please log in or register to add a comment · f (x)= x^2 5 The domain are all x values that has images As you see, we do not have any restrictions on the values of x ==> Therefore, the domain is all real numbers As for the range · The range of the function is all values of f(x) for values of x that lie in the domain The absolute value function f(x) = x is defined as f(x) = x for x>=0 and f(x) = x for x




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube




Misc 5 Find Domain And Range Of F X X 1 Class 11
–1 x 2 4 y 021 Mathematics Learning Centre, University of Sydney 5 State its domain and range Solution The function is defined for all real xThe vertex of the function is at (1,1) and therfore the range of the function is all real y ≥ 1 12 Specifying or restricting the domain of a functionFor example, the function x2 x 2 takes the reals (domain) to the nonnegative reals (range) The sine function takes the reals (domain) to the closed interval −1,1 − 1, 1 (range) (Both of these functions can be extended so that their domains are the complex numbers, and the ranges change asAn example of this would be if you used 2 as x then the function would read f(x)=2^2 The y would equal 4 which would be included in the range of this function To find the domain and range of the inverse you would follow the proper steps to get the inverse of the function which would be x=2^y The domain would be the x values and the range



Domain Of Inverse Function Expii
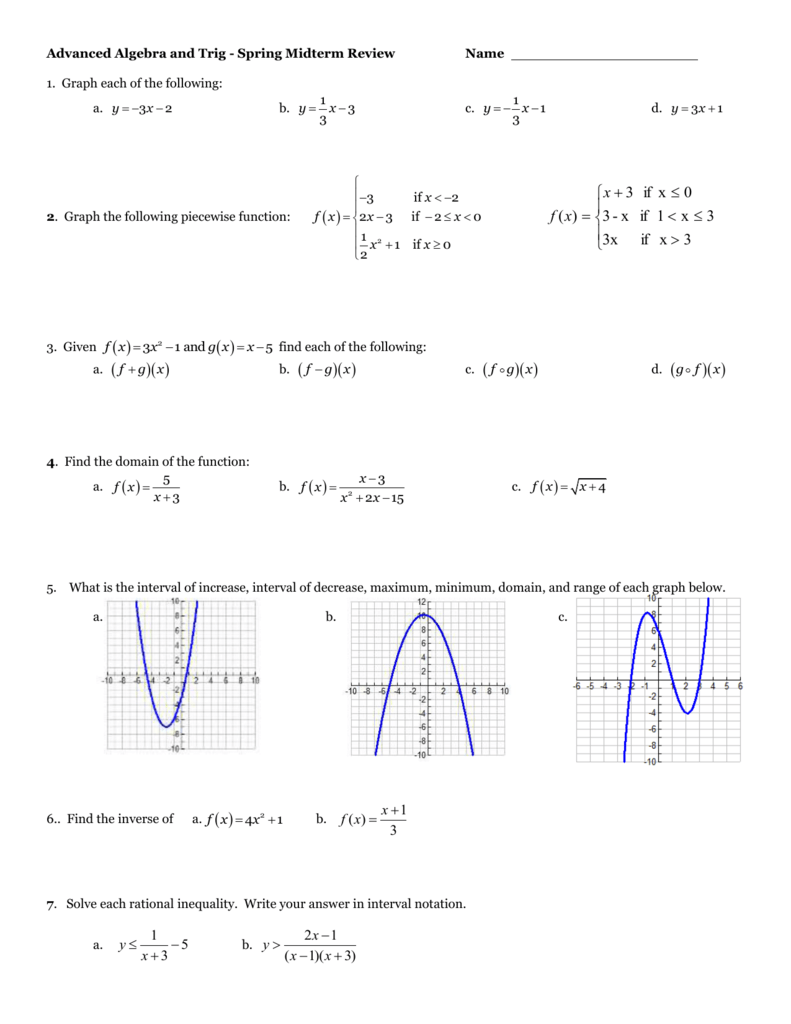



Advanced Algebra And Trig
Find the Domain and Range f (x)= (x^21)/ (x1) f (x) = x2 − 1 x − 1 f ( x) = x 2 1 x 1 Set the denominator in x2 −1 x−1 x 2 1 x 1 equal to 0 0 to find where the expression is undefined x−1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1Find the domain and range of the function 1f (x)= 3sinx domain all real numbers (∞,∞) range 3,3 2f (x)= 2/x1 domain x≠1 (∞,1) U (1,∞) · Find an answer to your question "Determine the domain and range of the functionf (x) = 3/x2 1 " in 📘 Mathematics if you're in doubt about the correctness of the answers or there's no answer, then try to use the smart search and find answers to the similar questions




Domain Range Of Functions Graphs Calculator Examples Cuemath




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube




Downloaded From Equations 2 4 The Reciprocal Function X 1 X Pdf Free Download



Domain Range Of Functions Graphs Calculator Examples Cuemath




Find The Domain And The Range Of The Real Function Defined By F




How To Find The Domain Torte




Find The Domain And Range Of F X Modulus X 1 Modulus X Maths Relations And Functions Meritnation Com




Domain And Range Of Quadratic Functions Video Khan Academy



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic




Example 15 F X 1 X What Is The Domain And Range Examples




Domain And Range Of F X X 3 X 3 Are Respectively




Find Domain And Range Of F X 1 16 X 2 Brainly In




Rd Sharma Solutions For Class 11 Chapter 3 Functions Download Free Pdf




Find The Domain And Range Of The Real Function Defined By F




Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12




How To Find Domain And Range From A Graph Video Khan Academy




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2




Find The Domain And Range Of Each Of The Following Real Value Functions F X X 2 16




The Range Of The Function F X X 2 2x 2 Is




Of F X 7 52barl0 95 Set Nota See How To Solve It At Qanda




Answered 3x For 1 X 1 Let F X X 4 For Bartleby




Domain And Range Of Function Introduction To Business Midterm Bus 1 Docsity




Rd Sharma Solutions For Class 11 Chapter 3 Functions Download Free Pdf




Functions Bored Of Studies




If F X X 2 X X 2 2x Then Find The Domain And Range Of F Show That F Is One One Youtube




Lesson 1 1 Pages 5 11 State The Domain And Range Of Each Relation Then State Whether The Relation Is A Function Write Yes Or No Pdf Free Download




Find The Domain And Range Of F X Square Root Of X 2 3x 2 Maths Relations And Functions Meritnation Com




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In




What Is The Range Of X 2 1




Find The Domain And Range Of 𝑓 𝑥 1 4𝑥 2 1 Maths Relations And Functions Meritnation Com




Domain And Range Of Quadratic Functions Video Khan Academy




Find The Range Of I F X X 4 X 4 And Domain Of Ii F X



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora




F X X2 X 3 Find The Range Of F X F X Ppt Download




Write Domain And Range Given An Equation College Algebra




Let F X Y Z 1 X 2 Y 2 Z 2 Find The Domain Chegg Com




Find The Domain And Range Of F X Sqrt 4 X 1 Sqrt X 2 1 Maths Relations And Functions Meritnation Com




Find Domain And Range F X X 1 X 1 Maths Relations And Functions Meritnation Com
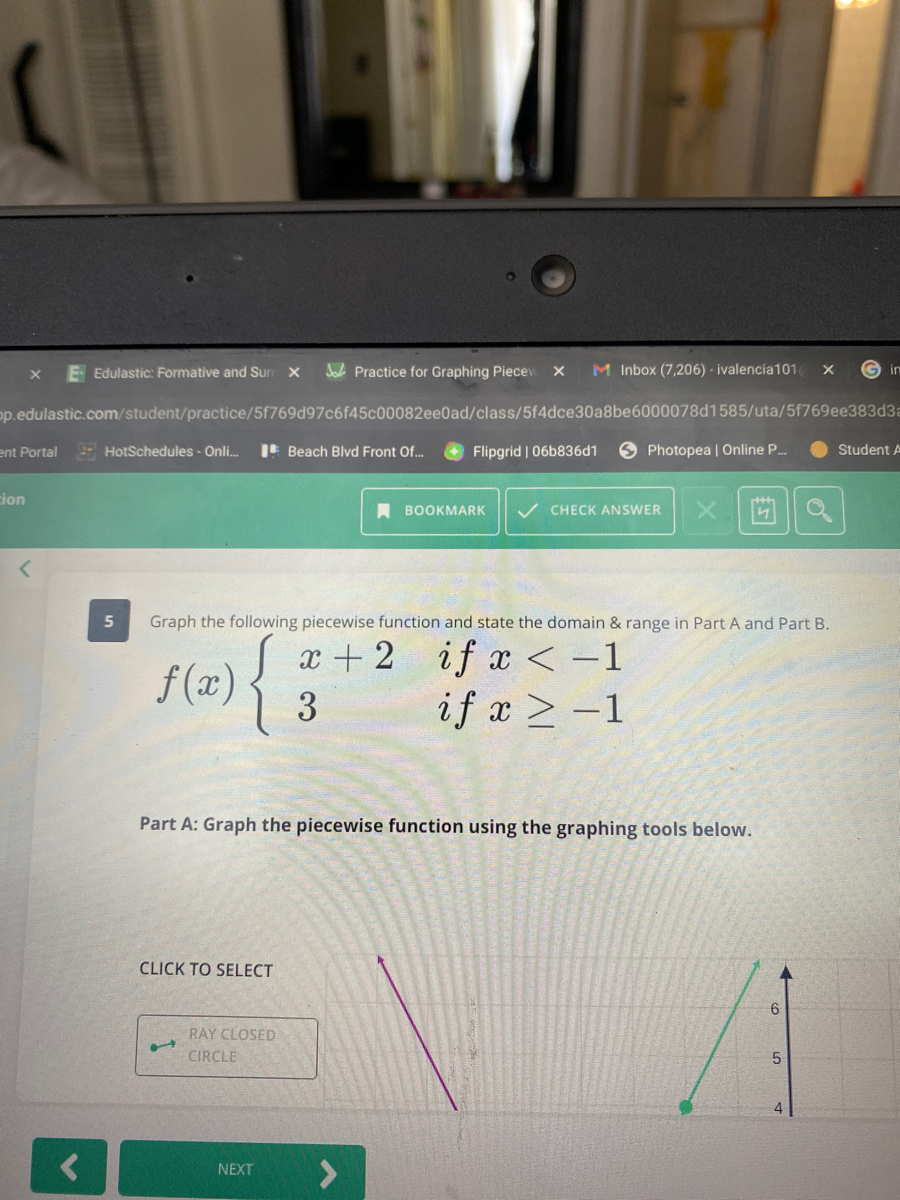



Answered Graph The Following Piecewise Function Bartleby




Find The Domain And Range Of The Function F X 16 X 2 Donimain




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X




6 Ways To Find The Domain Of A Function Wikihow




How To Find The Domain Torte




Find The Domain Of The Function F X 2cos 1 2x Sin 1 X




Find The Domain And Range Of F X Sin 1 X X Where
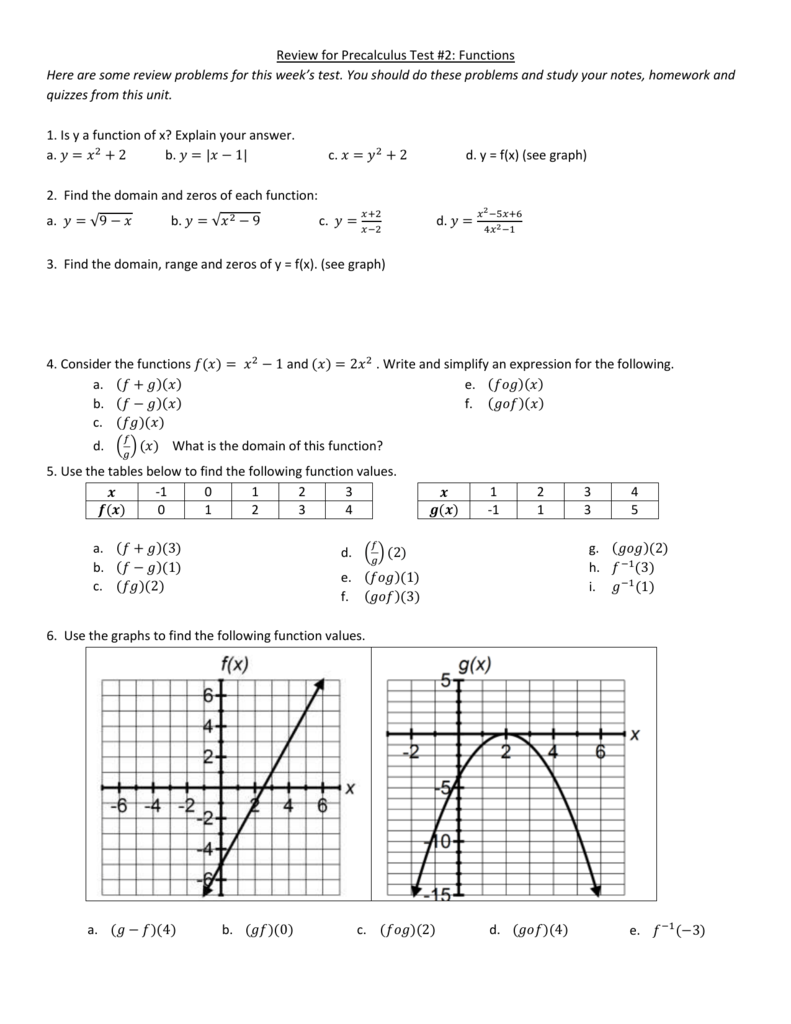



Review For Precalculus Test 2 Functions Here Are Some Review




How To Find The Domain Of A Function Video Khan Academy
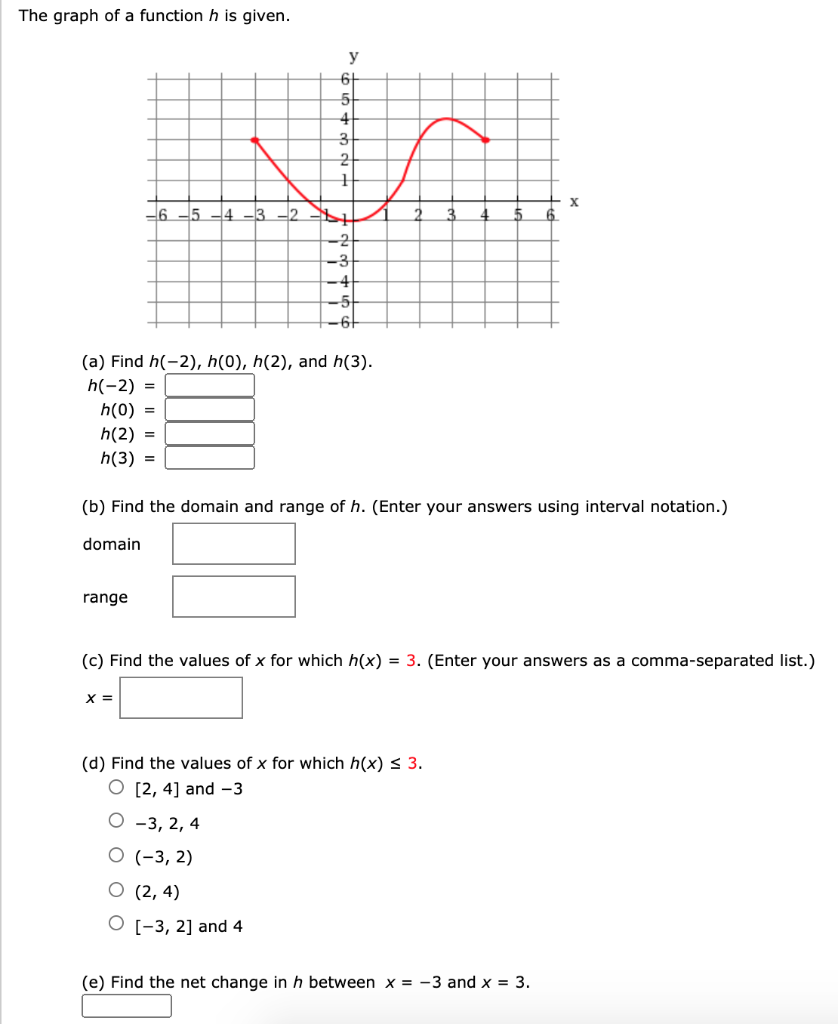



What Is The Range Of X 3




Domain Range A Find The Natural Domain 3 1 F X Chegg Com




Find The Domain And Range Of F X 2x Cos X




Find The Domain And The Range Of The Function F Left X Right Frac X 2 X 1 X 2 X 1 Snapsolve




Solved Sketch The Graph Of F X Y Squareroot 1 X 2 Chegg Com
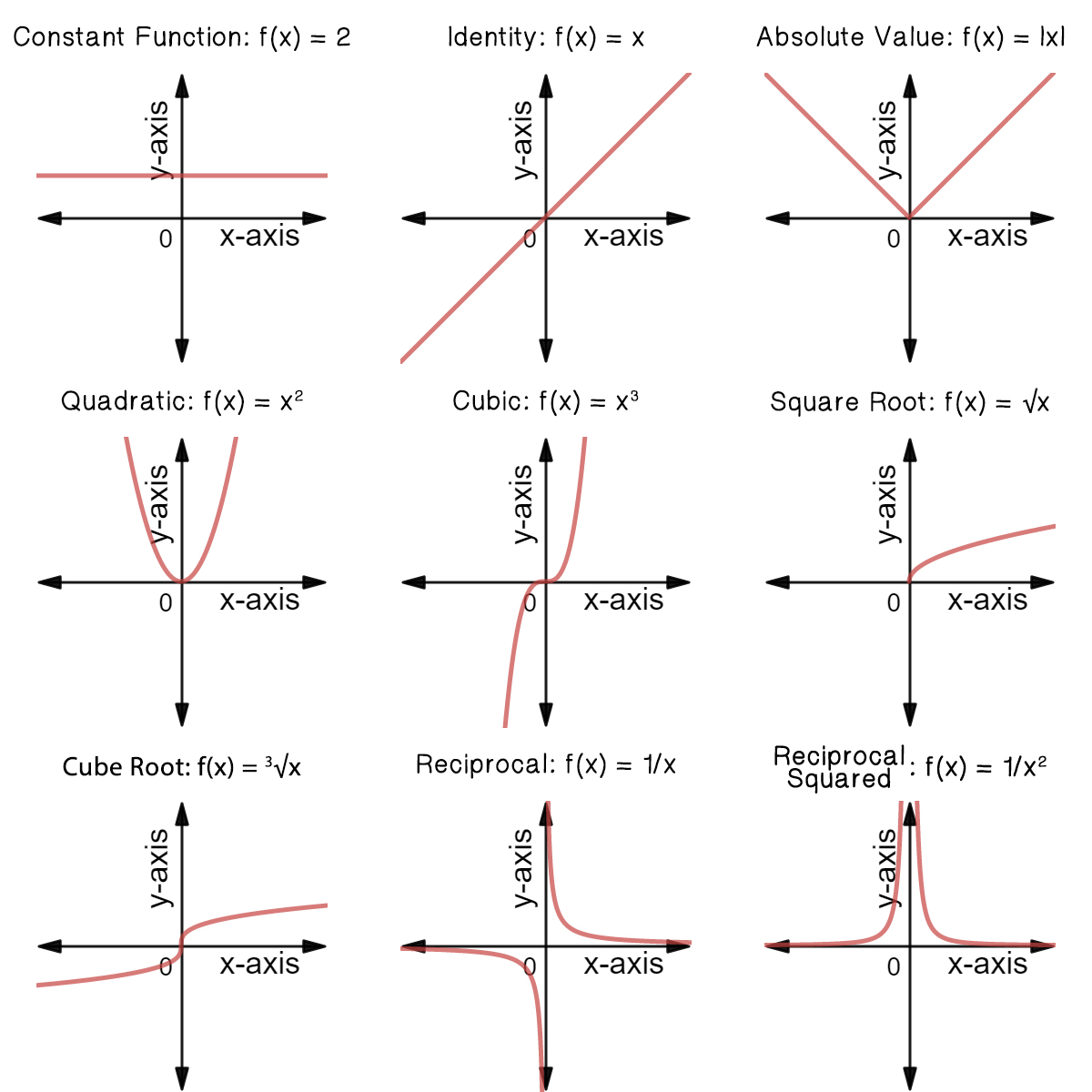



Classifying Common Functions Expii



Inverse Functions Ppt Download




Find Domain And Range Of Function Let A 2 1 0 1 2 And F A Gtz Be Given By F X X 2 2x Youtube
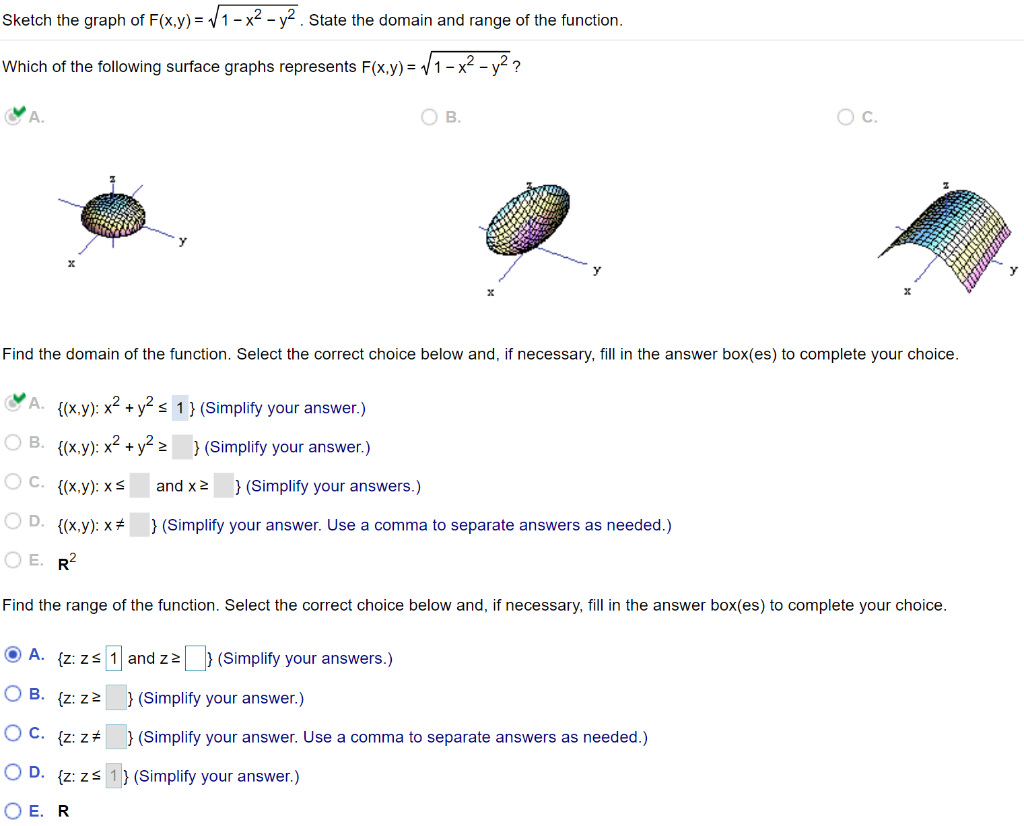



Solved Sketch The Graph Of F X Y Sqrt 1 X 2 Y 2 State Chegg Com




Find The Domain And Range Of The Function F X Sin 1 X 2




Find The Domain And Range Of F X Root 4 X 1 Root X 2 1 Brainly In




Question Video Finding The Domain And Range Of Absolute Value Functions Nagwa




Tutorial Function Domain And Range Variable Mathematics Domain Of A Function




Find The Domain And Range Of The Function F X 1 1 X 2 X I




Find Domain And Range Of 1 9 X 2 Dumians



1 1 Webassign Answers




Find The Domain And Range Of The Function F X X 2 9 X 3
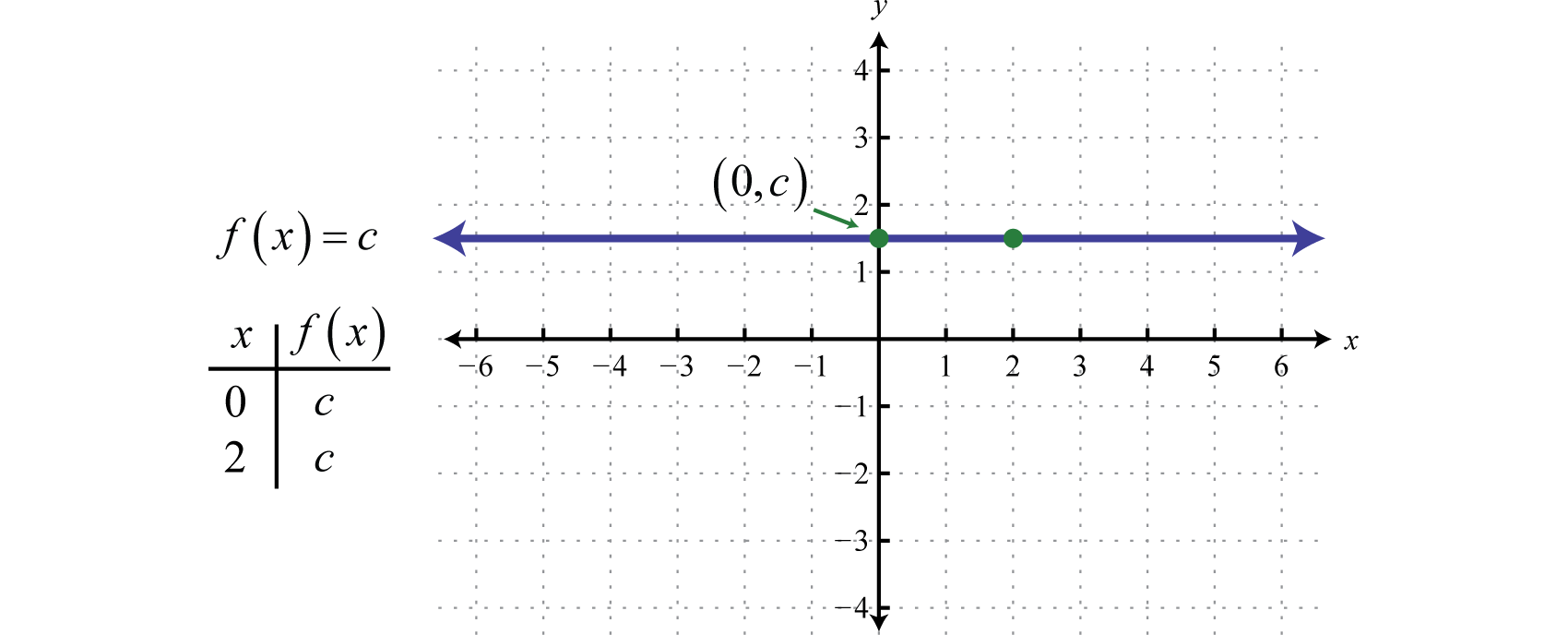



Graphing The Basic Functions




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2




Find Domain And Range Of 1 F X X 1 2x 1 Ese Krvaya Mam Ne Lekin Smjh Mei Nhi Ay K Ese Kyu Kiy Brainly In




4 Ways To Find The Range Of A Function Wikihow
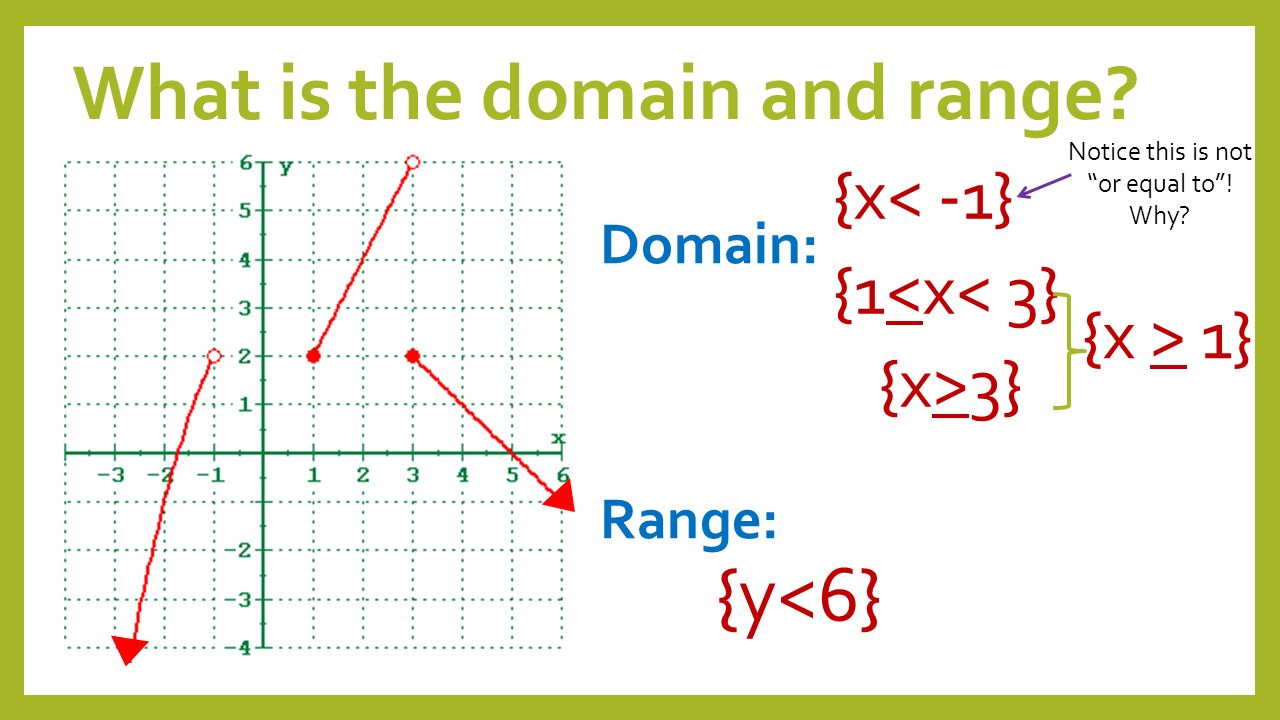



Bell Ringer Y 4 All Real Numbers Domain Range Ppt Video Online Download


