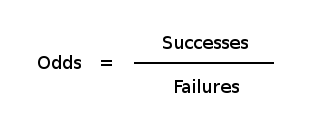
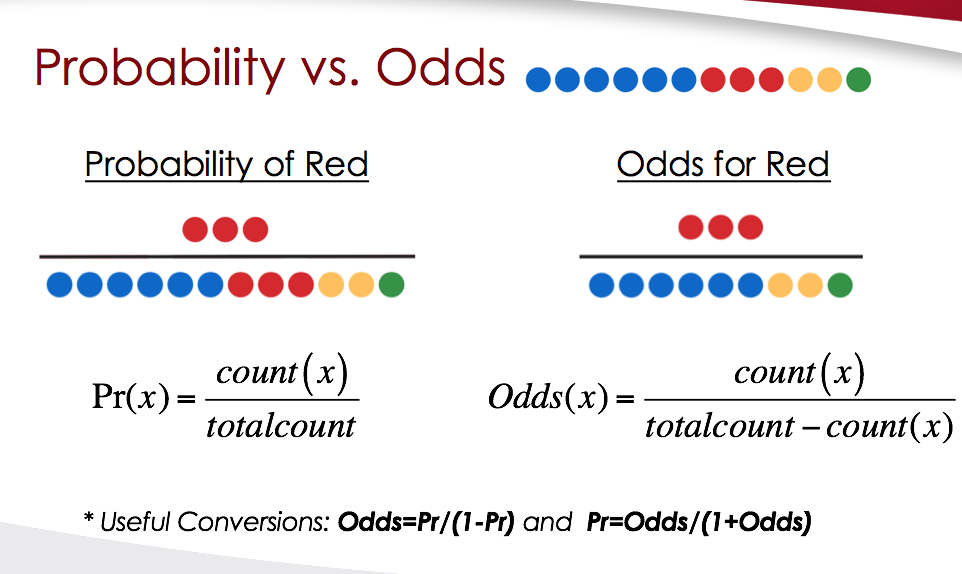
The probability that an event will occur is the fraction of times you expect to see that event in many trials Probabilities always range between 0 and 1 The odds are defined as the probability that the event will occur divided by the probability that the event will not occur If the probability of an event occurring is Y, then the probability of the event not occurring is 1YFor converting odds to probability, we have to divide the odds by 1 odds For instance, let's convert odds of 1/9 to a probability Now, divide 1/9 by 10/9 toOut of 5 times, 1 time will be the event and 4 times will be the nonevent, odds = 025 Odds = 1/5 / 4/5 = 1/4 = 025;
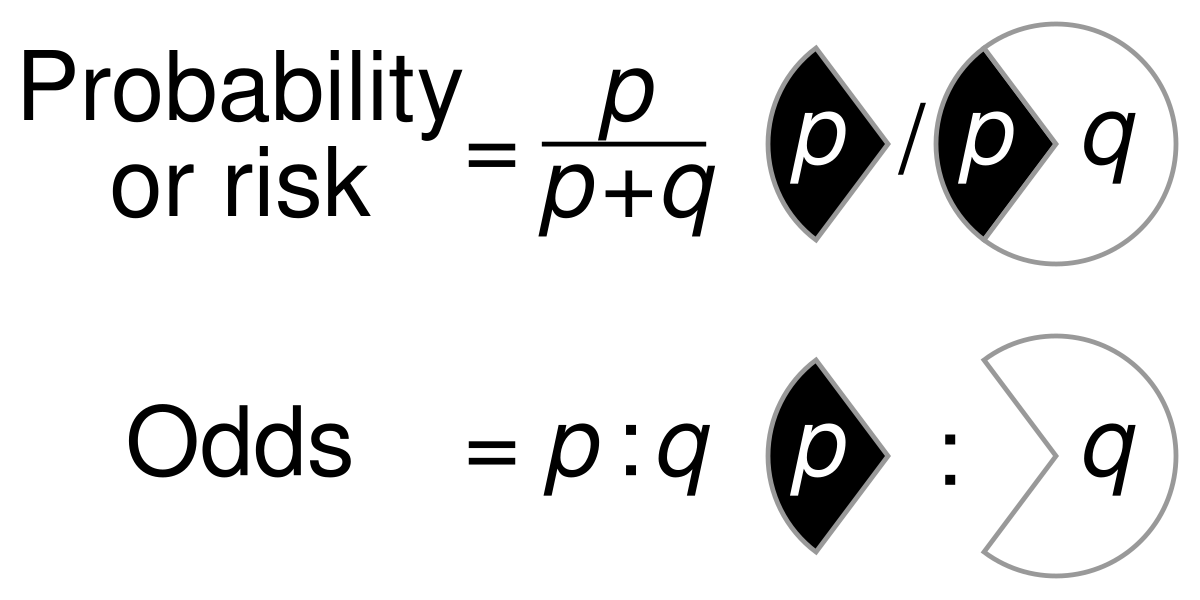
File Probability Vs Odds Svg Wikimedia Commons
Odds vs probability
Odds vs probability-Odds The odds in favor of an event is the ratio of the number of ways the outcome can occur to the number of ways the outcome cannot occur # of ways the event CAN occur # of ways the event CANNOT occur This is actually a lot easier than(35) = 3/8 = 375% Converting Probability to Odds Take the probability, and divide it by its compliment = (1itself) eg
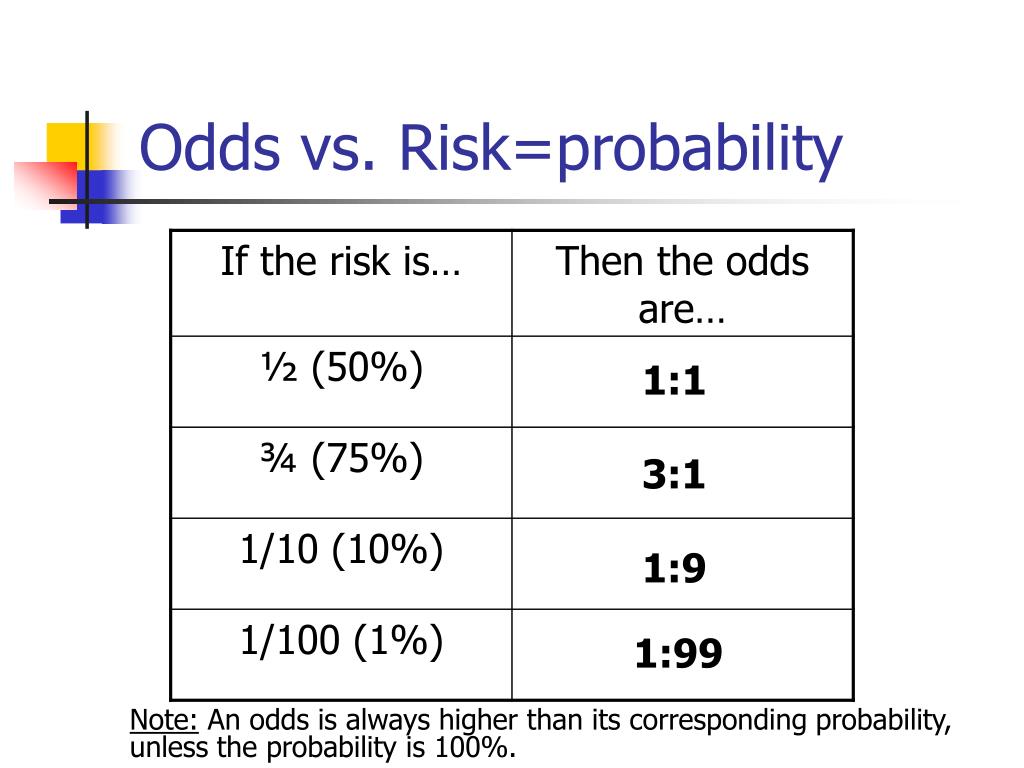



Ppt Conditional Probability Powerpoint Presentation Free Download Id
Statistics — Probability vs Odds 📅 Probability and odds are two basic statistic terms to describe the likeliness that an event will occur They are often used interchangeably in causal conversation or even in published material However, they are not mathematically equivalent because they are looking at likeliness inTo convert odds to probability, take the player's chance of winning, use it as the numerator and divide by the total number of chances, both winning and losing For example, if the odds are 4 to 1, the probability equals 1 / (1 4) = 1/5 or % Odds of 1 to 1 (50%) are called "evens," and a payout of 1 to 1 is called "even money"This video explains the difference between odds and probability This video is provided by the Learning Assistance Center of Howard Community College For mo
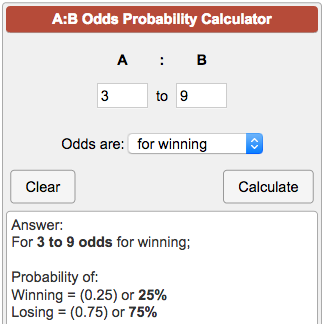
Posttest probability = Posttest odds / (Posttest odds 1) Fagan nomogram 3 The relation can also be estimated by a socalled Fagan nomogram (shown at right) by making a straight line from the point of the given pretest probability to the given likelihood ratio in their scales, which, in turn, estimates the posttest probability at the pointThe chance of winning is 4 out of 52, while the chance against winning is 48 out of 52 (524=48) Entering A=4 and B=48 into the calculator as 448 odds are for winning you get For 4 to 48 odds for winning;Calculating the odds without the number of subjects by the ratio of the number of events (1) by the number of nonevents (4) odds = 1/4 = 025;
Odds vs Probability Probability is a mathematical assumption of chance that can be calculated using an equation The equation measures the chances for an event to occur against the total number of chances that occurrence may produceIf the probability of success is 5, ie, 5050 percent chance, then the odds of success is 1 to 1 The transformation from probability to odds is a monotonic transformation, meaning the odds increase as the probability increases or vice versa Probability ranges from 0 and 1 Odds range from 0 and positive infinityOdds Odds seems less intuitive It is the ratio of the probability a thing will happen over the probability it won't In the spades example, the probability of drawing a spade is 025 The probability of not drawing a spade is 1 025 So the odds is 025/075 or 13 (or 033 or 1/3 pronounced 1 to 3 odds) Moving back and forth
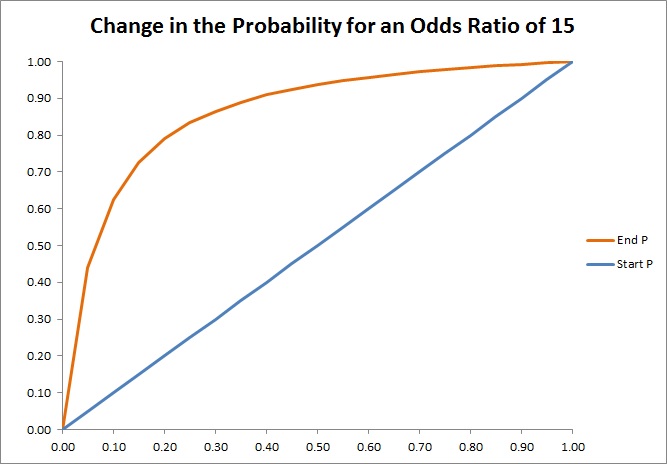



How To Convert Odds And Units To Probability Convert Odds To Percentage




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science
Probability of Winning = () or % Losing = () or %The Ask Dr Math forum has several entries on odds versus probability Summarizing, one way to conceptualize (nontechnically) the probability of an event is the number of ways that an event can occur divided by the total number of possible outcomes The probability of heads in a fair coin flip is 1/2 (50 percent)Odds ratio vs probability ratio Ask Question Asked 1 year, 8 months ago Active 7 months ago Viewed 647 times 8 5 $\begingroup$ An odds is the ratio of the probability of an event to its complement $$\text{odds}(X) = \frac{P(X)}{1P(X)}$$ An odds ratio (OR) is




Probability Vs Odds What S The Deal With State Lottery Odds Table




Ppt Conditional Probability Powerpoint Presentation Free Download Id
So a probability of 0 means there's literally no chance of that thing happening, a probability of 05 means there's a 50% chance, and a probability of 1 means that it's certain to happen As you can see, the idea of probability is relatively simple But the idea of odds, on the other hand, is a bit more complicatedmostly because thereAmerican odds are sometimes called moneyline odds and are accompanied by a plus () or minus () sign, with the plus sign assigned to the lower probability event with the higher payoutThe probability of P occurring is x in y the odds of P occurring are x to yx the odds against P occurring are yx to x Also, in can be replaced with out of or division, and to can be replaced with a colon So in your example, you have an event with probability 1/6 That's the same as saying 15 odds, or 51 odds against




7 Facts About Probability And Odds That You Don T Know



Probability Odds Lessons Blendspace
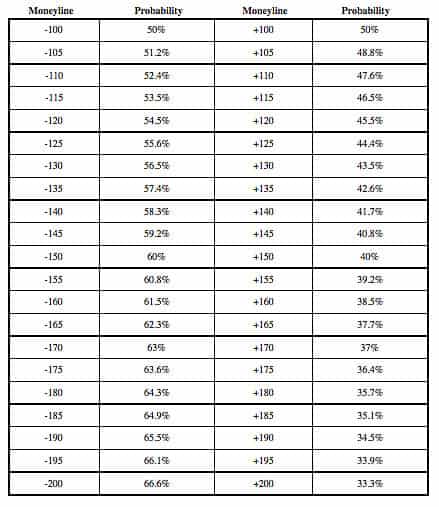
First, we have a simple calculator that you can use to plug in any moneyline (American style odds) and quickly get the fair market probability that it implies We've also included a chart below the calculator for reference, and to see how favorites and underdogs compare Money Line Calculator (Implied Probability)Answer (1 of 5) From a mathematics standpoint, let's assume p = number of possible positive outcomes of an event q = number of possible negative outcomes of an event Therefore p q = total number of outcomes of an event The probability of a positive event occurring is pIt is important to note, however, that odds to not directly represent probability of an event occurring, but rather the ratio of events to nonevents in total Odds vs Probability A good way to understand the difference between odds and probability is to imagine rolling a die and hoping to land on a two The odds of rolling the two are 1 to 5




Difference Between Odds And Probability With Comparison Chart Key Differences



Odds Vs Probability Casino Spies
In this matchup, there is a big difference between the two odds, indicating a much higher probability of Duke winning the game and advancing to the next round of the NCAA TournamentOf probability, chances and odds are not the same For instance, the odds in favor of A are P(A) / P(Ac) = (3/4)/(1/4) = 3/1 It is said that the odds in favor of A are 31 or that A is an event twice as likely as "not A" Therefore, the odds of A occurring are expressed in the scale of the probability of "A not occurring"Calculating Probability Given Odds To calculate
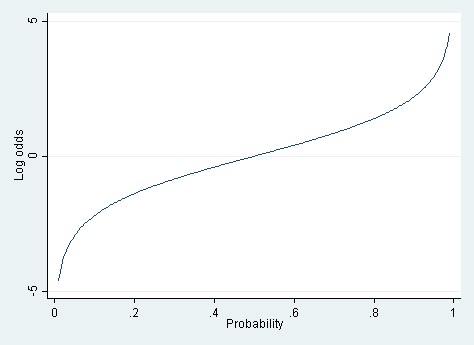



Linear Vs Logistic Probability Models Which Is Better And When Statistical Horizons



How Betting Odds Imply Probability
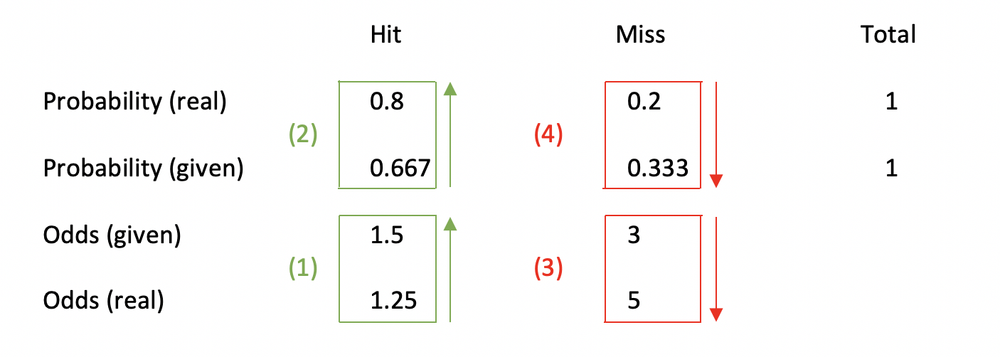
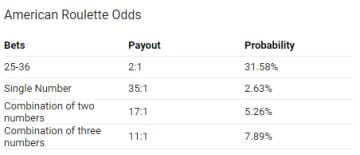
The odds are 1626 and probability is 016% If you're playing poker long enough you will somewhat regularly encounter the aces vs kings scenario at a table A formula to estimate the probability for this to happen at a 9 player table is This formula slightly underestimates the actual probability which is a little bit higherOdds are derived from a probability as follows (Boston University) If the probability of an event is 08 (ie an 80% chance), then the odds are 08 / (1 08) = 08 / 02 = 4, or 4 to 1 The following picture clarifies the difference between probability and odds, using an American roulette wheel with 18 black spaces, 18 red spaces, and 2Probability vs Odds Real life is full of incidents with uncertainty The terms probability and odds measure one's belief in the occurrence of a future event It may confuse since both 'Odds' and 'probability' are related to the potential that event occurs However, there is a difference Probability is a broader mathematical concept




Relation Between Probability And Odds At Different Values Of Probability Download Scientific Diagram



Why Do High Odds Mean A Low Chance Quora
The odds take the probability of an event occurring and divide it by the probability of the event not occurring So in the case of rolling a three on the first try, the probability is 1/6 that you will roll a three, while the probability that you won't roll a three is 5/6 The odds are represented by dividing these two probabilities 1/6 ÷Answer Since you carried out 67 trials and the number of 3s was 0, then the empirical probability of getting a 3 is 0/67 = 0, so the probability of not getting a 3 is 1 0 = 1 In a greater number of trials there may be an outcome of a 3Figure2 Odds as a fraction Odds should NOT be confused with Probabilities Odds are the ratio of something happening to something not happeningIn our scenario above, the odds are 4 to 6 Whereas, Probability is the ratio of something happening to everything that could happenSo in the case of our chess example, probability is 4 to 10 (as there were 10 games
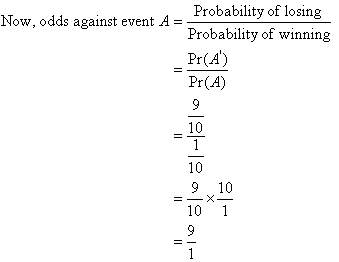



Odds




Converting Between Probability And Odds Mathwoes Youtube
$\begingroup$ @tpb261 41 is given as the odds, not probability $\endgroup$ – M Vinay May 30 '14 at 508 $\begingroup$ Ok, I understood the OP differently But Bayes' rule is for probabilities not odds For odds, they first have to be converted to probabilities $\endgroup$ – tpb261RELATIONSHIP OF RISK AND ODDS In the example above, for the same data set, the chances of death appear markedly different when expressed as risks and odds Table 2 shows the risk and odds for different event rates As "a" decreases with respect to "b" (probability of outcome becomes less), the odds and risk are similarHow to find probability and odds and the difference between the two We also discuss experimental probablility, theoretical probability, odds in favor, and




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios




Probability And Odds Youtube
Odds conversion table with probability Must be a number greater than 1 Must be a fraction, for example 2/1 Must be or and a whole number over 100 Must be a number from 0100 By convention only a set of fractions are used in fractional odds betting markets The set does not include exact mathematical equivalents to all possibleEqual odds are 1 1 success for every 1 failure 11 Equal probabilities are 5 1 success for every 2 trials Odds can range from 0 to infinity Odds greater than 1 indicates success is more likely than failure Odds less than 1 indicates failure is more likely than success Probability can range from 0 to 1Probability = 1/5 = 02;



Odds Vs Risk Vantage Research




9 2 Binary Logistic Regression R For Health Data Science
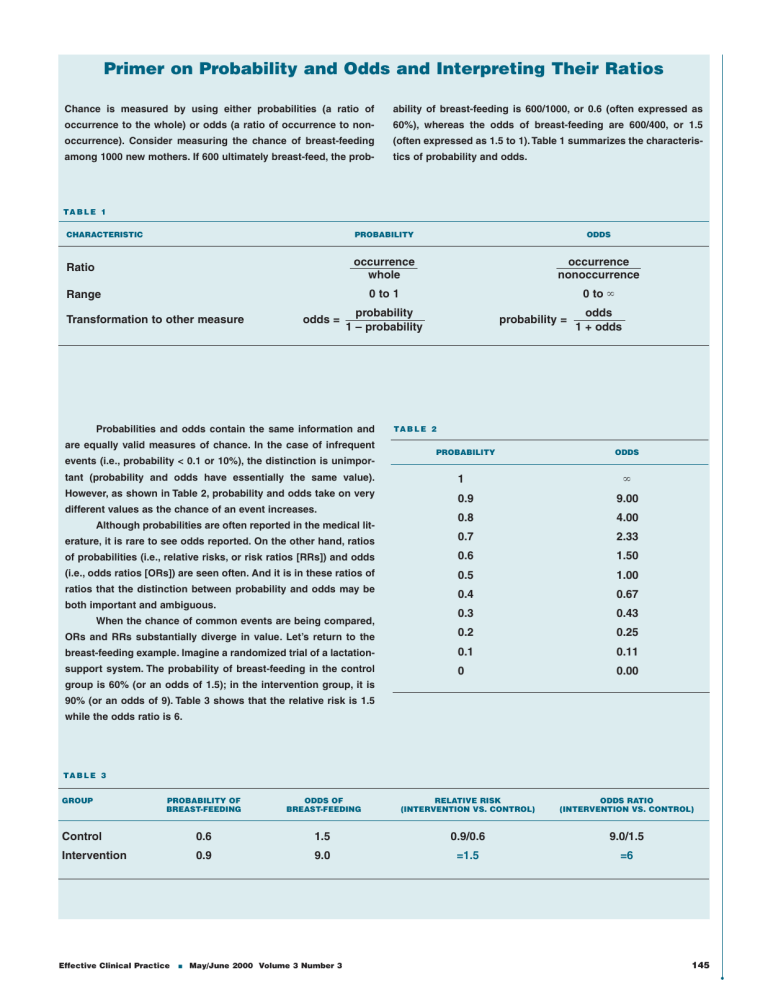
The primary difference between odds and probability is that while odds is a ratio of occurrence to nonoccurrence, the probability is the ratio of occurrence to the whole Odds are expressed in the ratio, the probability is either written in percentage form or in decimalIn the lower, I varied the values of the p parameter The probability distribution function isUnderstanding odds conversion to the percentage and implied probability behind the odds on offer is key to assessing the potential value in a particular betting market And it is just as important when assessing the value that exists with



What Are Odds The Right Way To Look At Odds For Sports Betting




Learn Odds In Favour And Odds Against In 3 Minutes
The probability that an event will occur is the fraction of times you expect to see that event in many trials Probabilities always range between 0 and 1 The odds are defined as the probability that the event will occur divided by the probability that the event will not occur A probability of 0 is the same as odds of 0In statistics, odds are an expression of relative probabilities, generally quoted as the odds in favorThe odds (in favor) of an event or a proposition is the ratio of the probability that the event will happen to the probability that the event will not happen Mathematically, this is a Bernoulli trial, as it has exactly two outcomesIn case of a finite sample space of equally likely outcomesProbability/Odds Conversion Converting probabilities into odds, we simply divide the probability by 1 less the probability, eg, if the probability is 25% (025), the odds are 025/075, which can also be expressed as 1 to 3 or 1/3 or 0333




Bayes Theorem Is Used To Calculate The Probability Of An Outcome




What Is A Probability And What Are Odds Core Im Podcast
$\begingroup$ I think the odds of a horse who has a 66% chance of winning would be 1/2 , meaning you get your bet back plus 1/2 the bet What you describe above is a probability 33% horse, get bet back plus 2x the bet Essentially youConverting Odds to Probability Simply add the 2 components of the odds together to make a new denominator, and use the old numerator eg If the odds are 35, or 3 to 5, the probability is 3 ÷Probability is defined as the percentage of desired outcomes against any possible outcomes within set rules For example, there's a 50% chance a coin will land on "heads" Odds which we hear a lot in sports betting, on the other hand, can have a value of 0 to infinity, and represent a ratio for desired and undesired outcomes



Primer On Probability And Odds And Interpreting Their Ratios




Odds And Likelihood Ratios Likelihood Ratios Can Help In By Anthony B Masters Oct 21 Medium
Figure 1 The binomial probability distribution function, given 10 tries at p = 5 (top panel), and the binomial likelihood function, given 7 successes in 10 tries (bottom panel) Both panels were computed using the binopdf function In the upper panel, I varied the possible results;Odds is a see also of probability As nouns the difference between odds and probability is that odds is the ratio of the probabilities of an event happening to that of it not happening while probability is the state of being probable;Playing 2 vs 1 dice I get around a % win rate Now to my problem, if I want to calculate the amount needed to always win as the house, the odds of losing (for the player) needs to be higher than the potentialwinningriskamount



The Difference Between Probability And Odds




Probability And Odds Quiz 13 Questions By Amy Harrison Tpt
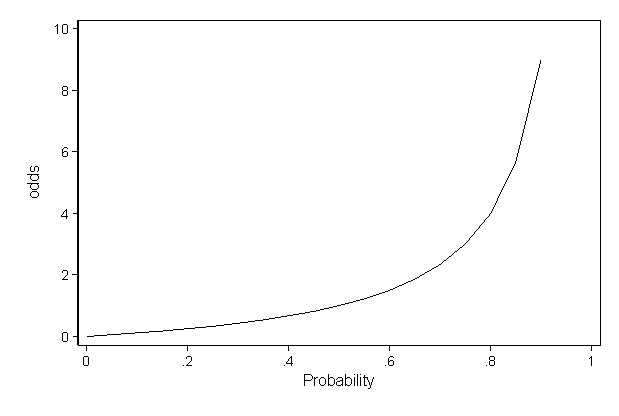
FAQs on Odds Vs Probability 1 How do you convert odds to probability?Labs(title =probability versus odds) 000 025 050 075 100 0 50 100 150 odds p probability versus odds Finally, this is the plot that I think you'llfind most




Lecture 5 Basic Probability David R Merrell 90




11 6 Probability Involving Or And Not



Odds
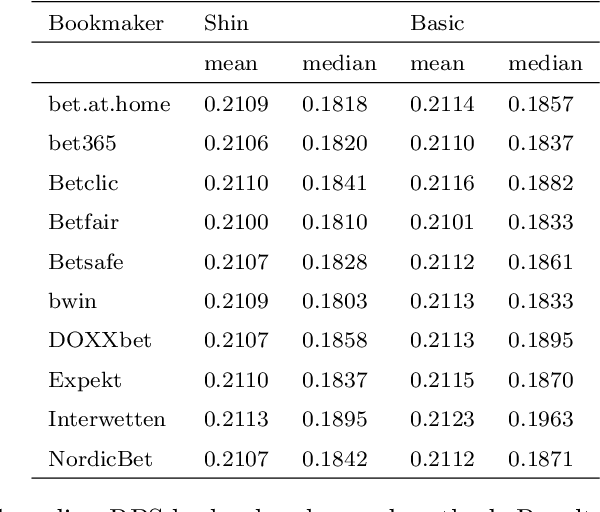



Pdf On Determining Probability Forecasts From Betting Odds Semantic Scholar




11 6 Probability Involving Or And Not




The Odds Against A Solving A Certain Problem Are 4 To 3 And The Odds In Favour Of Solving The Same Problem Are 7 To 5 Find The Probability That The Pr



Odds Probability And The Lottery Lotterycodex



Odds Probability Calculator




Solved The Probabilities Of Events A B And A Intersection Chegg Com




Relation Between Probability And Odds At Different Values Of Probability Download Scientific Diagram




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1




Odds And Probability




Comparing Probability Odds For And Odds Against Youtube




What Are The Odds Stats With Cats Blog




What S The Difference Between Probability And Odds




Math 30 2 Probability Odds Acceptable Standards 50 79 The Student Can Express Odds For Or Odds Against As A Probability Determine The Probability Ppt Download




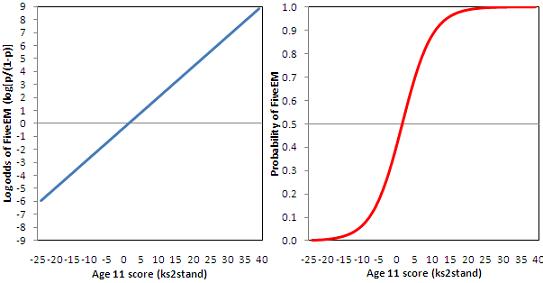
Logistic Regression 1 From Odds To Probability Dr Yury Zablotski




Pdf On Determining Probability Forecasts From Betting Odds Semantic Scholar
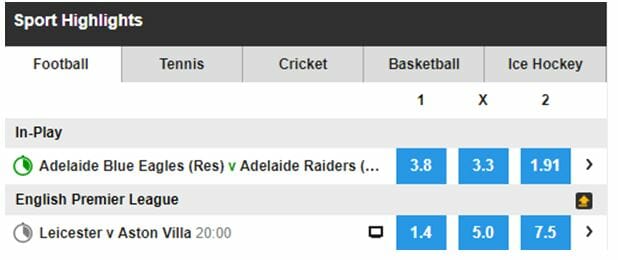



Implied Probability Betting Math Made Simple 21 Update




Good Odds Statistics And Probability Workbook Education Com Workbook Gre Math Free Workbook



1




Section 11 6 Odds And Expectation Math In Our World Ppt Download




Simple Probability Definition Probability The Chance Some Event



Week 1 Data Acquisition Ebm Flashcards Memorang



What Is The Probability Of Event E If The Odds In Favor Of E Is 10 21 Quora




How To Calculate Odds Ratios And Probabilities In Case Control Studies Cross Validated




How To Calculate Odds 11 Steps With Pictures Wikihow




Betting Fundamentals Understanding Probability Punting Stars



Relative Risk Ratios And Odds Ratios




The Difference Between Relative Risk And Odds Ratios The Analysis Factor



Why Saying A One Unit Increase Doesn T Work In Logistic Regression Learn By Marketing
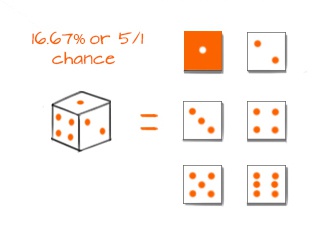



Betting Odds Explained Sport Betting Guide 8sport



1




Webinar Recording Signup




Is There A Difference Between Odds And Probability
:max_bytes(150000):strip_icc()/dotdash_Final_The_Math_Behind_Betting_Odds_and_Gambling_Nov_2020-01-735accb453c8424b9e063c2c14e4edf4.jpg)



The Math Behind Betting Odds Gambling




5 6 Probability And Odds Lesson




What Is A Probability And What Are Odds Core Im Podcast




Odds And Probability




Ppt Counting And Probability Powerpoint Presentation Free Download Id



Faq How Do I Interpret Odds Ratios In Logistic Regression




Probability And Odds By From The Hart 18 Teachers Pay Teachers



Odds Probability The Difference Explained With Examples




Odds Ratio The Odds Ratio Is Used To Find The By Analyttica Datalab Medium



4 5 Interpreting Logistic Equations




What Is An Odds Ratio And How Do I Interpret It Critical Appraisal




Advanced Bet School Understanding The Maths Behind Odds What They Mean For Your Chances Of Winning Futaa Com South Africa




Calculating Probability And Odds How To Find The Odds Of Casino Games



Probability Probability Vs Odds Lesson Math Statistics Showme
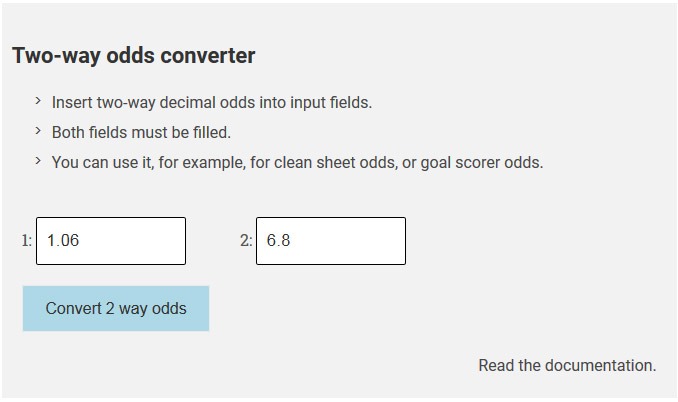



True Odds Calculator Find Probabilities Fair Odds Margin



2




File Probability Vs Odds Svg Wikimedia Commons




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science




2 6 Probability Vs Odds




Probability And Odds Math Odds Showme



Odds Vs Probability Vs Chance Data Science Central
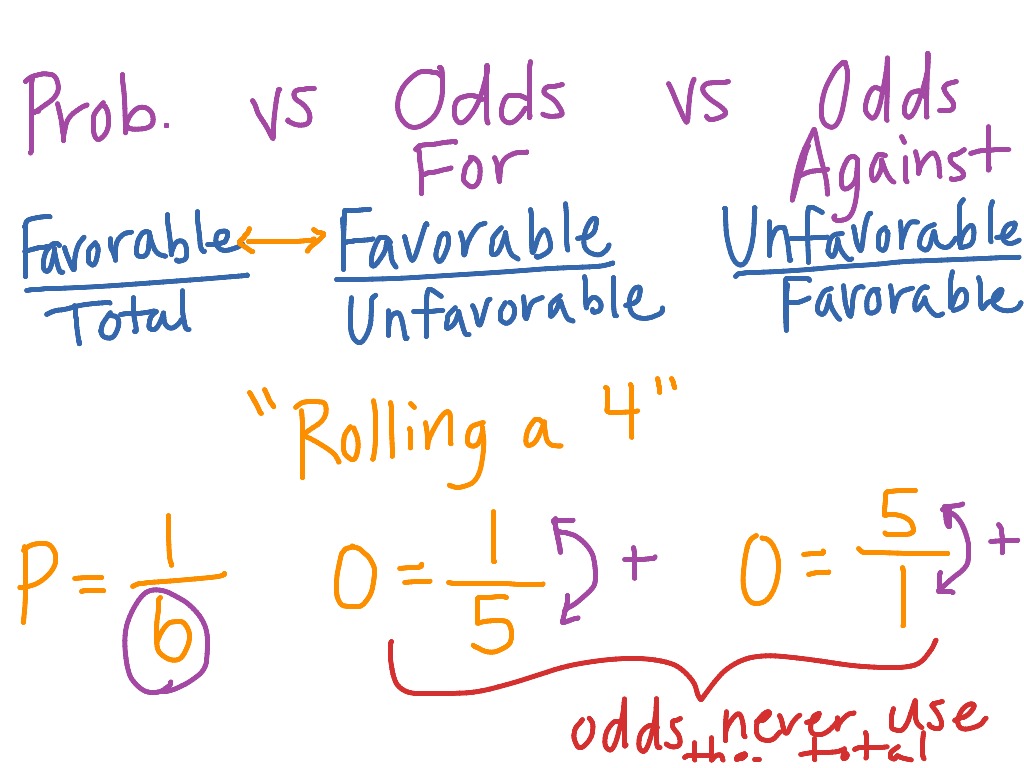



Odds Versus Probability Math Showme




What Are The Odds That You Know About The Odds Analytics Vidhya



2 Odds Ghci Grade 12 Mathematics Of Data Management



Introduction To Probability And Odds Acu Mathcasts




Probability And Odds Pptx Powerpoint



Odds Likelihood Ratios Guide To Diagnostic Tests




What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science




Odds Vs Probability What S The Difference Ask Difference




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science




Odds Are Not The Same As Probabilities Will Townes




Odds And Probability Definitions Key Difference Between Odds And Probability Comparison Chart Examples Ccss Math Answers




Learn Odds In Favour And Odds Against In 3 Minutes
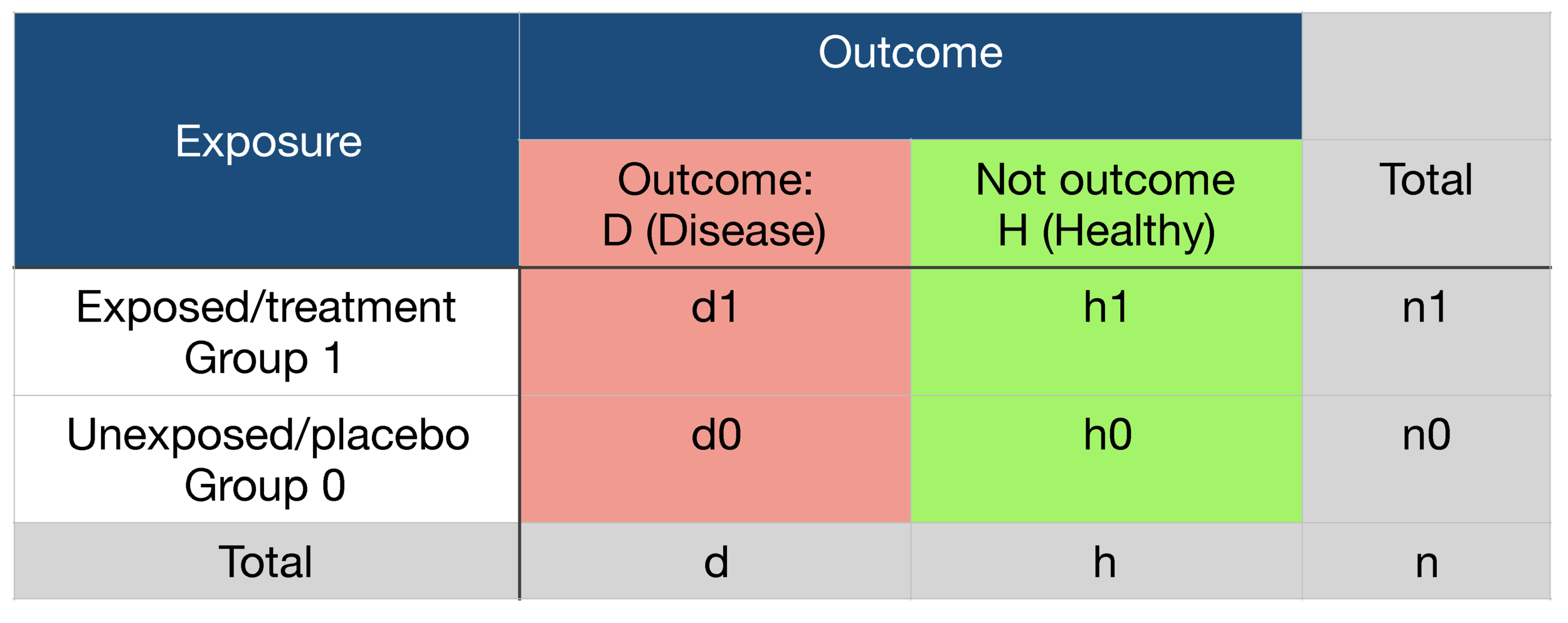



Probability Odds Ratio And Relative Risk Gpraj
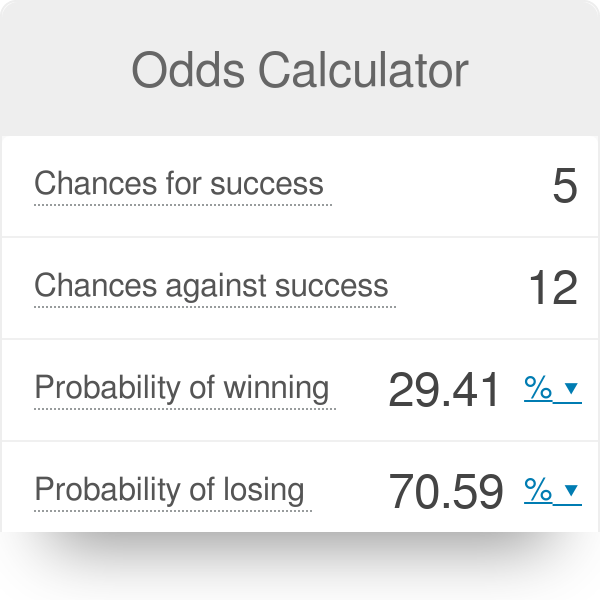



Odds Calculator



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1



Odds
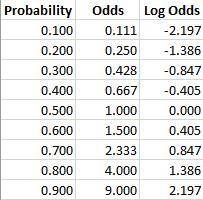



Log Odds Definition And Worked Statistics Problems




Probability Vs Odds In Favour Or Against An Event Examples Youtube



2 Odds Ghci Grade 12 Mathematics Of Data Management




Binary Logistic Regression With Odds Ratios Calculated For The Download Table



Odds Converter Convert Betting Odds



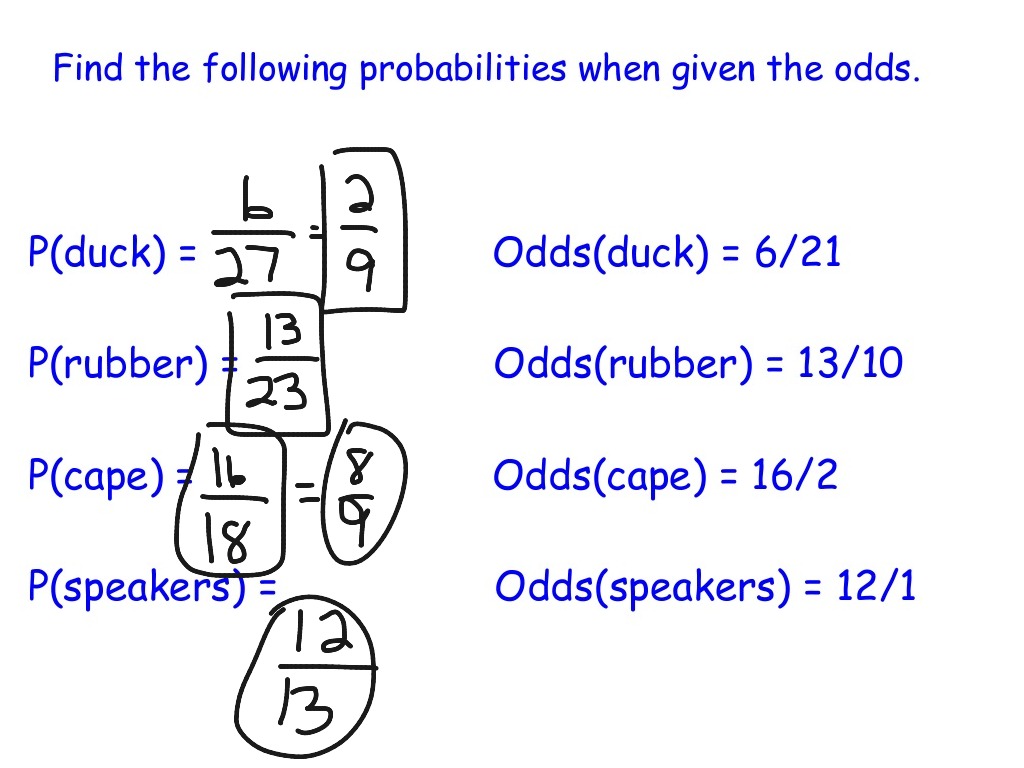
Worksheet Probability And Odds Number Cubes Dice Marbles Pre Algebra Printable


